[알고리즘] 삽입 정렬(Insertion Sort) 구현(C++, Python)
카테고리: Algorithm Theory
1. 🔍 삽입 정렬(Insertion Sort)의 개념
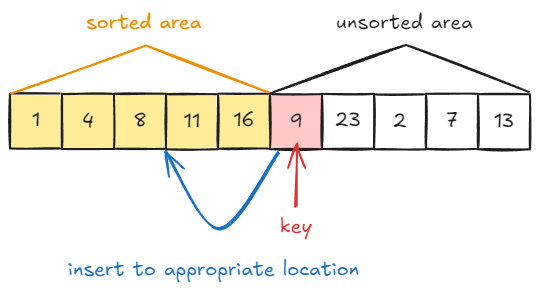
삽입 정렬은 데이터의 전체 영역에서 정렬된 영역과 정렬되지 않은 영역을 나누고 정렬되지 않은 영역의 값을 정렬된 영역의 적절한 위치로 놓으며 정렬한다.
- 그림으로 보면 다음과 같다.
- 그림을 보면 정렬되지 않은 영역에서 맨 앞에 있는 데이터 9를 정렬된 영역의 적절한 위치로 넣으며 오름차순으로 정렬한다.
- 정렬되지 않은 영역의 맨 앞에 있는 값을 키(key)라고 부른다.
- 키 값을 정렬된 영역에서 적절한 위치로 찾아 삽입하는 과정을 반복한다.
2. 💡 삽입 정렬의 동작 과정
- 최초에는 정렬된 영역은 왼쪽 1개, 정렬되지 않은 영역을 나머지로 한다.
- 정렬된 영역의 맨 끝 값부터 첫 값까지 순서대로 키와 비교하며 다음을 처리한다.
- 키보다 크면 해당 값을 오른쪽으로 한 칸 밀어낸다.
- 키보다 작거나 더 이상 비교할 값이 없으면 밀어낸 자리에 키를 넣는다.
- 모든 데이터가 정렬된 영역이 될 때까지 과정 2를 반복한다.
3. 🎨 그림과 함께 알고리즘 생각해보기
예시 그림과 함께 알고리즘을 생각해보자.
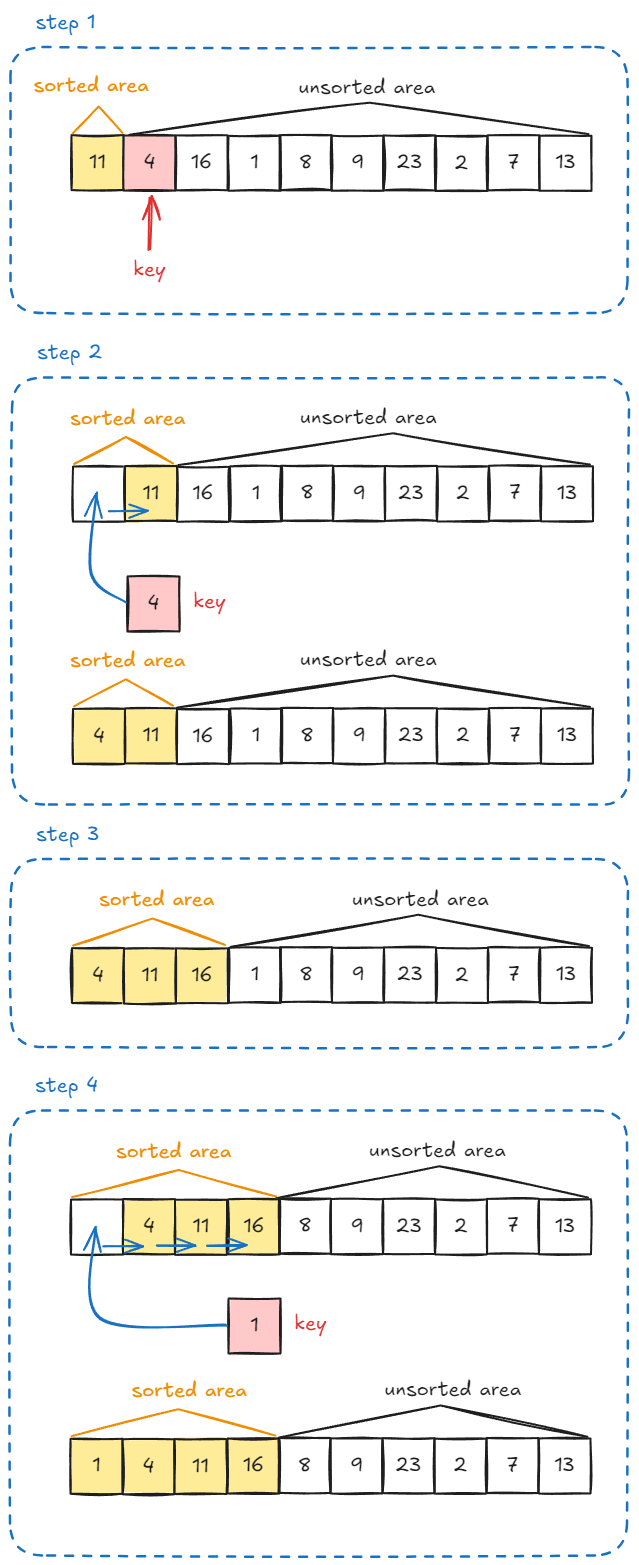
- 1단계: 최초의 데이터는 무작위로 배치되어 있다. 여기서 왼쪽 1개와 나머지를 각각 정렬된 영역과 그렇지 않은 것으로 생각한다.
- 2단계: 이제 정렬된 영역의 맨 끝 값부터 거슬러 올라가며 처리를 한다. 4와 11을 비교한다. 11이 크므로 11을 오른쪽으로 밀어낸다. 그러면 더 이상 비교할 값이 없으므로 4를 11을 밀어낸 자리에 넣는다.
- 3단계: 다음 키인 16을 보자. 11과 4를 거슬러 올라가며 처리를 진행한다. 11은 16보다 작다. 더 밀어내거나 할 필요 없이 16을 그대로 둔다.
- 4단계: 1은 16보다 작으므로 16을 밀어낸다. 최종적으로 모든 정렬된 값을 밀어내고 더 비교할 값이 없게 되므로 밀어낸 자리에 1을 넣는다.
- 5단계: 모든 데이터가 정렬된 영역이 될 때까지 반복한다.
4. ⚡ 삽입 정렬의 시간 복잡도
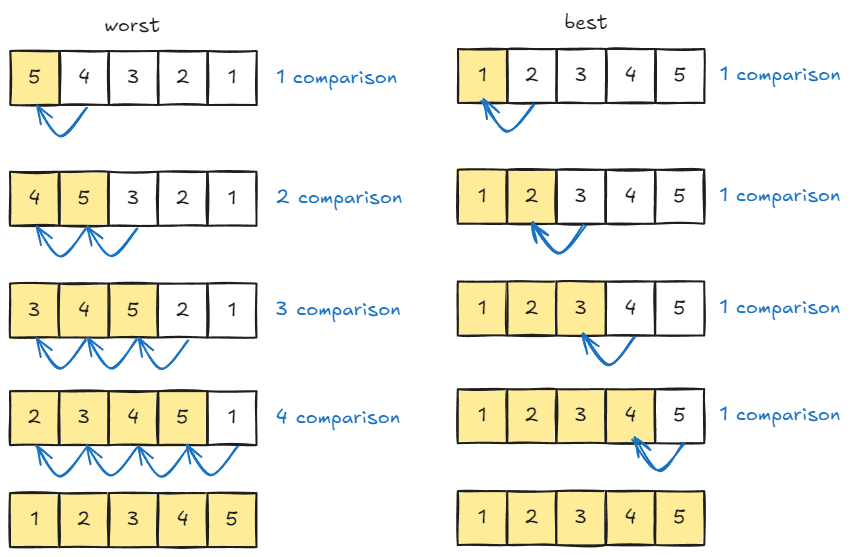
삽입 정렬의 시간 복잡도는 최악의 경우 $O(N^2)$이다.
- 최악의 경우는 데이터가 처음부터 의도한 정렬과 완전히 반대로 데이터가 저장된 경우이다.
- 정렬되지 않은 영역의 원소들을 정렬된 영역에 삽입할 때 정렬된 영역의 크기만큼 비교한다.
- 최선의 경우는 데이터가 이미 정렬되어 있어서 연산 횟수가 $N$이 된다. 시간 복잡도는 $O(N)$이다.
4.1 최악의 경우 시간 복잡도 계산
- 최악의 경우 시간 복잡도는 다음과 같이 계산한다.
4.2 최선의 경우 시간 복잡도 계산
- 최선의 경우 시간 복잡도는 다음과 같이 계산한다.
5. 📝 삽입 정렬의 구현
5.1. C++
#include <iostream>
#include <vector>
void insertionSort(std::vector<int>& arr) {
int n = arr.size();
for (int i = 1; i < n; i++) {
int key = arr[i];
int j = i - 1;
// 현재 키보다 큰 요소를 오른쪽으로 이동
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = key; // 키를 적절한 위치에 삽입
}
}
int main() {
std::vector<int> arr = {12, 11, 13, 5, 6};
insertionSort(arr);
std::cout << "Sorted array: ";
for (int i : arr) {
std::cout << i << " ";
}
std::cout << std::endl;
return 0;
}
5.2. Python
def insertion_sort(arr):
for i in range(1, len(arr)):
key = arr[i]
j = i - 1
# 현재 키보다 큰 요소를 오른쪽으로 이동
while j >= 0 and arr[j] > key:
arr[j + 1] = arr[j]
j -= 1
arr[j + 1] = key # 키를 적절한 위치에 삽입
if __name__ == "__main__":
arr = [12, 11, 13, 5, 6]
insertion_sort(arr)
print("Sorted array:", arr)